На основании пропорции золотого сечения был построен ряд чисел, замечательный тем, что каждое последующее число оказывалось равным сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 1З, 21 и т. д. Этот ряд был открыт итальянским математиком Фибоначчи и называется поэтому рядом Фибоначчи. Он обладает тем свойством, что отношения между соседними членами по мере возрастания чисел ряда, все более приближаются к 0,б18, то есть, к отношению золотого сечения.
Пропорции золотого сечения ученые связывают с развитием органической материи. Золотое сечение было обнаружено в объектах живой природы — в строении раковин, дерева, в расположении семян подсолнуха, в строении тела человека, а также его наблюдали в устройстве вселенной в расположении планет.
В отношении золотого сечения находятся так же элементы геометрических фигур — пятиугольника, звезды.

Точки пересечения линий, составляющих звезду, делят их
на отрезки в отношении золотого сечения.
В прямоугольнике золотого сечения стороны находятся в отношении золотого сечения. Этот прямоугольник содержит в себе квадрат и малый прямоугольник золотого сечения (его большая сторона является малой стороной первоначального прямоугольника).
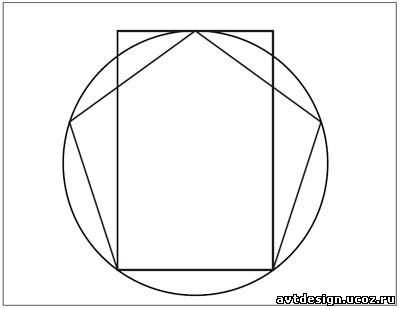
Прямоугольник приблизительно золотого сечения,
построенный на основании пятиугольника.
Поэтому можно построить прямоугольник золотого сечения на основании квадрата: сторона квадрата делится пополам, из той точки к вершине проводится диагональ, с помощью которой на стороне квадрата строится прямоугольник золотого сечения, как показано на рисунке:

Построение прямоугольника золотого сечения
на основе квадрата.
Этот малый прямоугольник подобен большому прямоугольнику, составленному из квадрата и малого прямоугольника золотого сечения, то есть оба эти прямоугольника являются прямоугольниками золотого сечения. Иначе говоря, если отсечь от прямоугольника золотого сечения квадрат, то остается меньший прямоугольник, стороны которого опять же будут находиться в отношении золотого сечения. Разбивая этот меньший прямоугольник на квадрат и еще меньший прямоугольник, мы опять получим прямоугольник золотого сечения, и так до бесконечности. Если соединить вершины квадратов кривой, то мы получим логарифмическую кривую, бесконечно растущую спираль, которую называют «кривая развития», «спираль жизни», ибо в ней как бы заложена идея бесконечного развития.
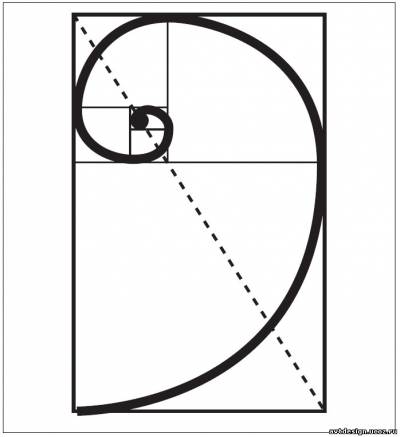
Логарифмическая кривая "Спираль жизни"
Бесконечное повторение прямоугольника золотого сечения и квадрата при рассечении прямоугольника золотого сечения обнаруживает повторение целого в его частях, что является одним из условий гармонии целого. Это свойство прямоугольника золотого сечения было обнаружено художниками и они стали употреблять золотое сечение как способ гармонизации, способ пропорционирования. Фидий использовал золотое сечение при постройке Акрополя (5 век до н. э.). Греческие ремесленники, создавая гончарные изделия также применяли золотое сечение. В эпоху Возрождения золотое сечение использовали не только в зодчестве, скульптуре, живописи, но и в поэзии и музыке. Дюрер, Леонардо да Винчи и его ученик Лука Пачоли применяли золотое сечение в поисках гармоничных пропорций букв.
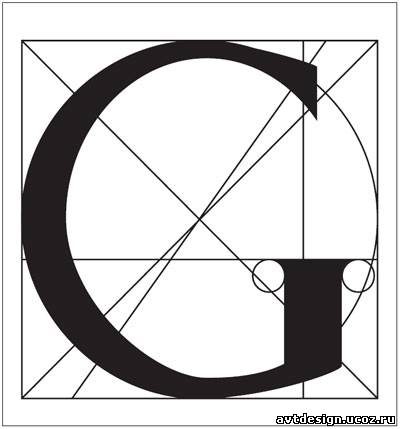
Построение буквы из книги Луки Пачоли
"О божественной пропорции"
Прямоугольник золотого сечения мы встречаем и в пропорциях средневековых рукописных книг, и в современной книге, так как стройные пропорции золотого сечения позволяют красиво организовать пространство книжной страницы и разворота.
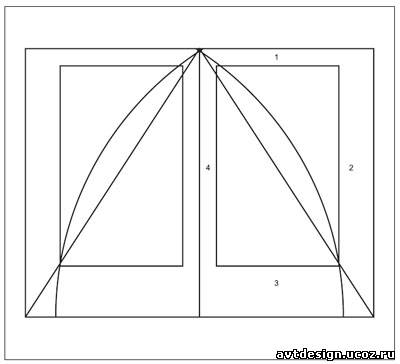
Схема идеальных пропорций средневековой рукописи.Пропорции страницы 2 : 3, а плоскость, занятая письмом - в пропорции золотого сечения.
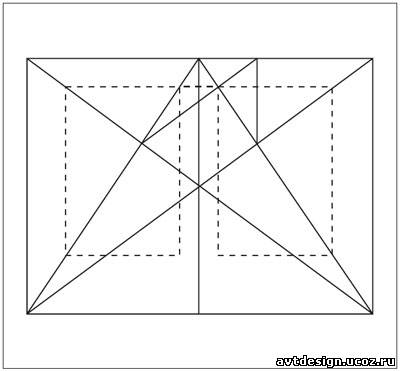
Один из способов определения размера
полосы набора при заданном формате.
Математические закономерности композиции. Пропорционирование.
| 
 Дизайн теория
Дизайн теория Регистрация
Регистрация Вход
Вход
