В композиционной структуре произведений искусства и дизайна имеют значение пропорции прямоугольников и других геометрических фигур, в которые вписывается данное произведение или его основные части. Поэтому следует рассмотреть прямоугольники, которые нашли наиболее широкое применение благодаря своим гармоническим свойствам (о прямоугольнике золотого сечения говорилось выше). Обратимся снова к квадрату. Квадрат как конструктивная форма известен издавна. Он привлекал внимание художников Древнего мира и эпохи Возрождения. На рисунке Леонардо да Винчи изображена связь квадрата и круга с человеческой фигурой известная еще древним, (Витрувий). Художники Возрождения — немец Дюрер, итальянец Пачоли, француз Тори, занимаясь разработкой начертания букв, исходили из формы квадрата, буква со всеми своими элементами вписывалась в квадрат, хотя и не все буквы приравнивались к квадрату, однако общий композиционный строй определялся квадратом.
Квадрат является устойчивой, статичной фигурой. Она ассоциируется с чем-то неподвижным, завершенным. В Древнем мире у некоторых народов изображение квадрата было связано с символикой смерти. (В этой связи интересно заметить, что пропорции квадрата в природе встречаются в формах неживой материи, у кристаллов).
Благодаря своей статической завершенности квадрат используется в прикладной графике, в области визуальных коммуникаций наряду с формой круга как элемент, фиксирующий внимание, а также для ограничения пространства, на котором сосредоточена информация.
Помимо прямоугольника золотого сечения и квадрата, наибольший интерес для нас представляют прямоугольники Ц2 и Ц5. Древние греки эпохи классики предпочитали именно эти прямоугольники, Хэмбидж утверждает, что 85% произведений греческого классического искусства построено на прямоугольнике Ц5. Чем интересен этот прямоугольник? Будучи разделенным по вертикали н по горизонтали на две части, он восстанавливает свои пропорции. Прямоугольник этот можно расчленить на квадрат и два малых прямоугольника золотого сечения. Кроме того, в нем просматриваются два прямоугольника золотого сечения, перекрывающие друг друга на величину квадрата. Оставшаяся часть тоже представляет собой прямоугольник золотого сечения. Таким образом, прямоугольник Ц5 обнаруживает ритмические свойства. В нем возникает красивая симметрия (малый пр-к з. с. + квадрат + малый пр-к з. с.).
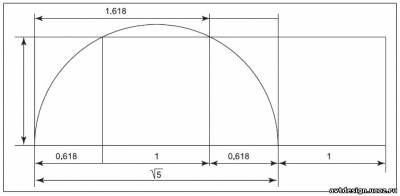
Ритмические свойства прямоугольника.
Хэмбидж приводит композиционную схему греческой чаши для питья из бостонского музея: чаша вписывается (без ручек) в горизонтально вытянутый прямоугольник Ц5. Диагонали двух прямоугольников золотого сечения, перекрывающих друг друга на квадрат, пересекаются в точке, через которую проходит граница между чашей и ее ножкой. Ширина основания ножки равна высоте чаши и равна стороне квадрата, находящегося в центре прямоугольника Ц5. Ножка вписывается в два малых прямоугольника золотого сечения, отсеченных от квадрата линией, горизонтальной к основанию прямоугольника Ц5 и проходящей через точку пересечения двух диагоналей больших прямоугольников золотого сечения.
В современном художественном конструировании прямоугольник Ц5 также находит широкое применение. Мы его встречаем в пропорциях автомашин, станков и других изделий. В прикладной графике — в форматах проспектов, буклетов, упаковок; в изобразительном искусстве, в монументальном искусстве, в пропорциях картинной плоскости, в композиционном строе картины.
Прямоугольник Ц2 также находит широкое применение, в осообенности в области прикладной графики. Он используется как формат бумаги для деловой документации, поскольку обладает удивительным свойством, — при делении пополам он не меняет своих пропорций. При делении образуется ряд подобных прямоугольников, гармонически связанных между собой единством формы.
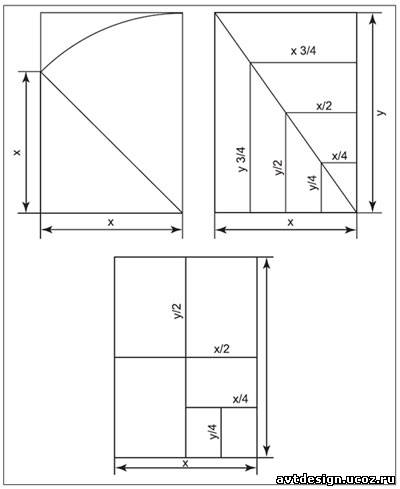
Пропорции сторон в прямоугольнике Ц2,
используемые в стандарте Поратмана.
На рисунке приводится изо6ражение прямоугольников, используемых при композиционном построении благодаря гармоническим отношениям их сторон:
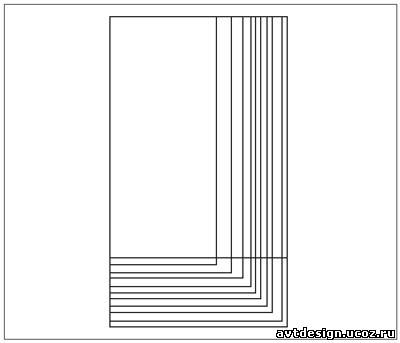
Гармонические отношения сторон в прямоугольниках.
Ниже приводятся числовые отношения прямоугольников Ц2, Ц3, Ц4, Ц5 к их обратным числам, с которыми они находятся в гармоническом отношении. (Обратным числом называется число, полученное при делении единицы на данное число). Если принять меньшую сторону прямоугольникака за единицу, то для прямоугольника Ц2 число (соответствующее большей стороне)=1,4142, а обратное число=0,7071; для прямоугольника Ц3 число=1,732, обратное число=0,5773; для прямоугольника Ц4 число=2, обратное число =0,5; для прямоугольника Ц5 число=2,236; обратное число=0,4472; для прямоугольника золотого сечения число= 1,618, обратное число=0,618.
На основе прка Ц2 была проведена стандартизация и унификация форматов книг, бумаг, деловой документации, открыток, плакатов, папок и других объектов, связанных с прикладной графикой. Этот стандарт, известный как стандарт доктора Порстмана был принят в 17 европейских странах. В основу стандарта был положен формат 841 х 1189мм и площадью в 1м2. От него выведены остальные форматы, составляющие его доли:
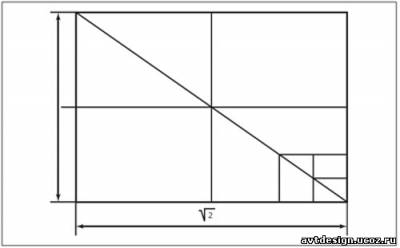
Деление прямоугольника на доли 1/2, 1/4, 1/8, 1/16, 1/64.
1 м² — 841 х 1189мм
1/2 м² — 594 х 841мм
1/4 м² — 420 х 594мм
1/8 м² — 297 х 420мм (двойной лист)
1/16 м² — 210 х 297мм (лист для деловой переписки, бланков)
1/32 м² — 148 х 210мм (поллиста для деловой переписки, бланков)
1/64 м² — 105 х 148мм (почтовая открытка)
1/128 м² — 74 х 105мм (визитная карточка)
Стандартом предусмотрены и дополнительные форматы 1000 х 1414 и 917 х 1297 и их доли. Для конвертов предлагаются размеры: 162 х 229 и 114 х162 (стандарт приведен не полностью).
Поскольку обращение с деловыми бумагами, документацией подразумевает необходимость иметь не только соответствующие им по размеру и формату конверты и папки, но и емкости, в которых хранится документация, отсюда возникает необходимость в соответствующей мебели: столах, шкафах, полках. Размеры и пропорции мебели, в свою очередь, подсказывают и характер интерьеров помещений. Таким образом возникает целостная система гармонизованных элементов интерьера, подчиненная единому модульному принципу.
Пропорциональные отношения должны существовать не только между отдельными частями целого, но и между предметами, составляющими группы объектов, связанных единым стилем, функциональной задачей. Например, между объектами, входящими в систему фирменного стиля.
Предметы, окружающие человека, должны быть гармонизованы не только по отношению друг к другу, но и связаны с человеком единой мерой, с физическим его строением. Зодчие древности считали, что отношение частей архитектуры друг к другу и к целому должно соответствовать частям человеческого тела, их отношениям. Таким же образом Модулор Корбюзье исходит из размеров человеческого тела и из отношений золотого сечения в нем (расстояние от земли до солнечного сплетения и расстояние от солнечного сплетения до макушки составляют крайнее и среднее отношения золотого сечения).
Масштабные отношения между вещами, предметным окружением и человеком выступают как средство гармонизации, ибо масштаб является одним из проявлений соразмерности, устанавливающим относительные раамеры между человеком и предметом — в архитектуре, в дизайне, в прикладном искусстве, в частности, в прикладной графике, в искусстве книги. Так, размеры и форматы плакатов и любых объектов, служащих целям визуальной коммуникации — вывесок, дорожных знаков и т. д., а также их композиционное решение всегда избираются в зависимости от назначения и от условий эксплуатацин, а значит и в соответствующих масштабных отношениях. То же самое касается и области книжного оформления и всевозможной печатной рекламы и упаковки.
Математические закономерности композиции. Симметрия. Гармония.
|

 Дизайн теория
Дизайн теория Регистрация
Регистрация Вход
Вход
